Le Monde Creux

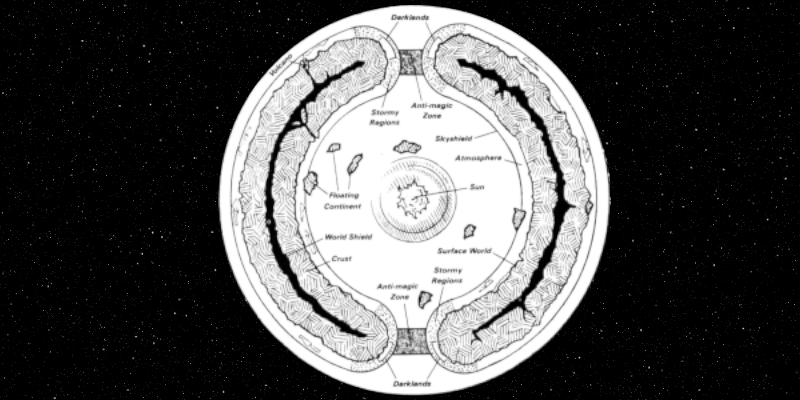
Même si nous n’envisageons pas d’utiliser, cartographier ou décrire la surface interieure de Mô’OmgaÏa, nous avons choisi de maintenir une forme de planète similaire à celle de Mystara : un monde creux (Hollow world). Dans ce post nous présentons la méthode utiliser pour la representation 3D de la planète.

Une fonction paramètrique

Pour Mystara, on a souvent tendance à simplifier en considérant un monde externe et un monde interne mais en réalité la surface est continue, celle du monde interne rejoignant celle du monde externe via des orifices prés des pôles. Le volume généré par cette surface est symétrique par rapport à l’axe passant par les centres des orifices. On peut donc dans un premier temps réduire le problème à une recherche de courbe 2D qui fera ensuite l’objet d’une rotation pour obtenir la surface ou le volume de la planète.

Pour assurer la continuité de surface, nous allons appréhender le problème (la définition de la courbe 2D) comme la recherche d’une trajectoire pouvant être décrite par une fonction paramètrique. Pour respècter la forme de Mystara/Mô’Omgaïa, cette fonction paramètrique fera appel à trois paramètres clé :

• le rayon nominal de la surface du monde externe, $R_{out}$;
• le rayon de l’arc d’ouverture entre le monde interne et externe, $R_{opening}$, autrement dit la demi-épaisseur du monde creux ou $R_{out} - R_{in}$, $R_{in}$ étant le rayon nominal de la surface du monde interne;
• l’angle d’ouverture défini entre les deux arcs d’ouverture, $\theta$.

La trajectoire est donné par $N$ points de contrôle $[t, x, y]$. Notons que le temps $t$ des points de contrôles ne suivent pas nécessairement une grille régulière. La seule hypothèse que nous faisons est que les points sont triés en fonction du temps ainsi $t[i] < t[i+1]$.

trajectory = {
 
  const polar_to_cartesian = ({r, theta}) => ({ x: r * Math.cos(theta), y: r * Math.sin(theta) })
  const cartesian_to_polar = ({x, y}) => ({ r: Math.sqrt(x * x + y * y), theta: Math.atan2(y, x) })
  const theta = Math.PI*((Math.sqrt(3)-1)/2);
  const n = 20;
 
  let pt1 = polar_to_cartesian({r:9.979*2, theta:theta});
  let v1 = ({x:pt1.x, y:pt1.y});
  let pt2 = polar_to_cartesian({r:4.668*2, theta:theta});
  let v2 = ({x:pt2.x, y:pt2.y});
  let pt3 = polar_to_cartesian({r:9.979*2, theta:-theta});
  let pt4 = polar_to_cartesian({r:4.668*2, theta:-theta});
  
  const radius = distanceTo(v1, v2)/4;
  const c1 = ({x:(pt1.x+pt2.x)/2,y:(pt1.y+pt2.y)/2});
  const c2 = ({x:(pt3.x+pt4.x)/2,y:(pt3.y+pt4.y)/2});
 
  var points = [];
 
  const traj = (a1, a2, center, step, r) => {
    var points = [];
    d3.range(a1, a2, step).map(i => {
      let ptXY = polar_to_cartesian({r:r*2, theta:i});
      points.push( {x:ptXY.x + center.x, y:ptXY.y + center.y} );
    })
    return points;
  }
 
  const pts1 = traj(-theta, theta, {x:0, y:0}, 2*theta/n, 9.979);
  const pts2 = traj(theta,theta+(n-2)*Math.PI/n, c1, (2*theta/n)*9.979/radius, radius);
  const pts3 = traj(theta,-theta, {x:0, y:0}, -(2*theta/n)*9.979/4.668, 4.668);
  const pts4 = traj(-theta-(n-2)*Math.PI/n,-theta, c2, (2*theta/n)*9.979/radius, radius);
  const N = pts1.length + pts2.length + pts3.length + pts4.length + 1;
 
  return ({
    knots:[...pts1, ...pts2, ...pts3, ...pts4, pts1[0]].map((pt,i)=>[i/N, pt.x, pt.y]), 
    circles:[{center:{x:0, y:0}, radius:2*9.979}, {center:{x:0, y:0}, radius:2*4.668}, {center:c1, radius:radius*2}, {center:c2, radius:radius*2}, {center:{x:0, y:0}, radius:9.979+4.668}]
  })
  
}

Pour améliorer la résolution de la courbe, on utilise une fonction spline qui nous permet d’interpoler la trajectoire entre chaque doublet de points de contrôle. On obtient ainsi une fonction dépendante de $t$ permettant de calculer la position $(x,y)$ à un temps donné.

spline = {
  var ts = trajectory.knots.map(([t,x,y]) => t);
  var xs = trajectory.knots.map(([t,x,y]) => x);
  var ys = trajectory.knots.map(([t,x,y]) => y);
  
  var X = NaturalCubicSpline(ts, xs);
  var Y = NaturalCubicSpline(ts, ys);
  return (t) => [X(t), Y(t)];
}

Maintenant que nous avons une fonction paramètrique pour décrire la section de la planète nous pouvons passer à la 3D…

Représentation 3D

Nous utiliserons la librairie 3D écrite en javascript Three.js pour représenter ici notre planète en 3D.

La géométrie de la planète est construite sur la base d’un objet THREE.LatheGeometry dont les points sont calculés avec la fonction paramètrique interpolée. Le nombre de points utilisé depends du niveau de détails recherché qui est donné en argument.

mystaraGeometry = {
  const points = [];
  for ( let t = 0; t <= 1; t+=1/details ) {
    let pt = spline(t);
  	points.push( new THREE.Vector2( pt[0], pt[1] ));
  }
  return new THREE.LatheGeometry( points, details );
}